Dosier: Didáctica de las Matemáticas.
Un análisis político e ideológico sobre saberes y prácticas

Las fórmulas de área en clases de primaria, una muestra de las tensiones entre currículo y estudiantes

Introducción: una contradicción institucional entre la inclusión y los contenidos curriculares

En¹ una clase, la hoja de Flavio permanece en blanco, mientras sus compañeros ya encontraron el área de varias figuras trazadas sobre una hoja cuadriculada a través de diversos procedimientos. Cuando llega la observadora, Flavio intenta utilizar la fórmula para un triángulo, se equivoca y corrige con estimaciones a partir del conteo de cuadros. Más tarde, explica por qué antes no había ningún trazo en su hoja:

este… o sea, para mí contar cuadritos… yo lo quiero hacer bien, o sea, yo no quiero contar cuadritos (…) sino que yo lo quiero hacer bien (…) primero tengo que multiplicar (…) pero no puedo.

Flavio no recurre a los procedimientos que tiene a su alcance, como el conteo de unidades, porque no le parecen legítimos; tampoco recurre a la fórmula de área –aunque reconoce que tiene mayor jerarquía- porque le es ajena. Así, opta por quedarse al margen de la actividad. Este es un ejemplo que pone en blanco y negro el argumento que intentaré probar en este artículo: la pretensión de estudiar las fórmulas de área en el momento estipulado por el currículo, bajo las condiciones institucionales en las que se organiza su enseñanza –en particular, cuando las fórmulas se sostienen en conocimientos con los que buena parte de las y los alumnos todavía no cuentan y se enseñan a partir de libros de texto en los que prevalece la ostensión-,² aumenta la desigualdad entre estudiantes en términos de acceso a los conocimientos escolares y es uno de los factores que, en algunos casos, propician exclusión.

Hay una contradicción entre el propósito de dar cabida en la escuela a la participación de la totalidad de estudiantes y, simultáneamente, estipular desde el currículo una serie de contenidos para ser aprendidos en un tiempo determinado. Se trata de una de las múltiples características de la escuela, señaladas por Terigi (2009), que hacen que ésta contribuya al fracaso escolar, al recibir estudiantes para luego expulsarlos,³ y se configura desde las leyes en materia educativa. Desde 1993, la Constitución mexicana, en su artículo tercero, relativo a la educación, estipula que ésta no solo es gratuita y obligatoria, sino también un derecho, que debe ser garantizado con calidad. En 2019, se declaró también que la educación debe ser “inclusiva”. Por otro lado, desde 1917 hasta la fecha, se han ido agregando, de forma paulatina, preceptos a dicho artículo. La primera legislación contenía 71 palabras y se centraba en el carácter laico y gratuito de la educación, en cambio la de 2019 es un escrito de más de 2400 palabras, que contiene una gran lista de

principios inobjetables como el respeto a los derechos humanos, la perspectiva de género, la interculturalidad, la vida saludable, la música, la honestidad, la fraternidad, la inclusión, la integridad de la familia, la literacidad, la filosofía, la innovación, el pensamiento crítico, el cuidado del ambiente y la cultura para la paz (Rockwell, 2021, p. 15).

Este crecimiento paulatino del currículo se gesta en múltiples ámbitos, como los preceptos constitucionales, las leyes secundarias y estatales, los distintos niveles de la burocracia escolar, los planes y programas de estudio, los mecanismos de evaluación, los libros de texto y otros materiales escolares y las propuestas de formación docente (materiales y propuestas que provienen tanto de instancias gubernamentales como de la iniciativa privada). Todas esas instancias agregan nuevas exigencias -a veces contradictorias- a la enseñanza, que cada sector del aparato escolar interpreta y reelabora según sus trayectorias y condiciones de trabajo (Rockwell, 2021).

El fenómeno es añejo y amplio en términos geográficos; numerosos estudios llaman la atención sobre la tendencia a comprimir el currículo y agregarle cada vez más demandas sin suprimir otras (ver, por ejemplo, Chartier, 2004). Un ejemplo, puntual pero también claro, se puede ver en un folleto escrito en la década de 1940 por el ministerio de educación de Inglaterra:

Instead of the junior schools performing their proper and highly important function of fostering the potentialities of children at an age when their minds are nimble and receptive, their curiosity strong, their imagination fertile and their spirits high, the curriculum is too often cramped and distorted by over-emphasis on examination subjects [En lugar de que las escuelas primarias desempeñen su adecuada e importantísima función de fomentar las potencialidades de la infancia en una edad en la que sus mentes son ágiles y receptivas, su curiosidad es fuerte, su imaginación fértil y su espíritu elevado, el plan de estudios se ve con demasiada frecuencia estrechado y distorsionado por un énfasis excesivo en las materias objeto de examen] (Burke y Grosvenor, 2013, p. 152)

Sadovsky (en Grimaldi, 2021) destaca algunos efectos de la prescripción temporal del aprendizaje de contenidos en las organizaciones curriculares; entre ellos, que la preocupación de las y los docentes por la imposibilidad de cubrir el programa les obliga a suprimir algunos contenidos, o bien, a enseñarlos con rapidez. Ambas decisiones tienen consecuencias sobre los procesos de aprendizaje de las y los alumnos, lo cual incluso puede favorecer “ciertas interpretaciones que discapacitan a los alumnos que no se ajustan a estas expectativas” (Grimaldi, 2021, p. 427).

Como ya expliqué, en este texto me enfoco en el análisis de las tensiones entre el proceso de saturación del currículo y la educación inclusiva a partir de la observación de lo que ocurre en el aula con el estudio de uno solo de los innumerables contenidos curriculares: las fórmulas para calcular áreas de figuras geométricas.

Cuando se mira a la primaria desde la secundaria, o incluso desde el bachillerato o la universidad,⁴ las fórmulas de área son apenas una pequeña puerta de entrada al amplio mundo del álgebra. Pero, al observar de cerca lo que ocurre en la primaria y pensarla como una etapa valiosa por sí misma, el estudio de las fórmulas resulta más problemático. Las siguientes dos imágenes dan una idea fugaz sobre un rasgo común a las diferentes maneras de enseñar dicho contenido en las clases de matemáticas, y que ha perdurado a lo largo del tiempo:

Imagen 1

Imagen 2

La imagen 1 muestra una clase de aritmética de tercer grado en la escuela primaria Horace Mann, en Columbia, Estados Unidos, entre 1900 y 1905.⁵ La imagen 2 es la exposición de un equipo de alumnos en las clases que observé en 2017 en la Ciudad de México. En ambas aparece la expresión “base por altura sobre dos”, que se ejemplifica con un triángulo inscrito en un rectángulo.

Diversos trabajos muestran que la relación que existe entre el área del triángulo y el rectángulo, y las que subyacen a otras fórmulas de área, no son tan fáciles de comprender para las y los alumnos. En un estudio sobre prácticas de enseñanza en escuelas primarias mexicanas (Weiss, Block, Civera, Dávalos y Naranjo, 2019) se observó a quince docentes y se encontró que, en la asignatura de matemáticas, las clases en las que se abordaban procedimientos que apuntaban a las fórmulas para obtener el área o el volumen fueron las más problemáticas. Los autores atribuyen esto en buena medida a dificultades en el diseño de los libros de texto, que no logran llevar a buen término el propósito de que las y los alumnos contribuyan a reconstruir las fórmulas. Moreira Baltar (1996–1997) analiza los resultados de evaluaciones nacionales a estudiantes de primaria y secundaria en Francia. Menos del 50 % de las y los alumnos resolvió los reactivos concernientes al área. Por ejemplo, el 40 % de estudiantes que comenzaban sexto grado determinó el área de un rectángulo; dato significativo, pues de esa fórmula suelen derivarse las correspondientes a las otras figuras. Ella interpreta que el origen de los errores está en el tratamiento escolar, que ubica los problemas de superficie ya sea en el marco geométrico o en el numérico –con tendencia a privilegiar el segundo-; pero no existe un trabajo de integración de ambos, que resulta esencial para la comprensión del área y, en particular, para el uso de fórmulas.

En este artículo trataré de acercarme a lo que hay detrás de esos datos a partir de un estudio didáctico y etnográfico para el cual observé dieciocho clases de matemáticas, dedicadas principalmente a las fórmulas de área, en un grupo de quinto grado de una escuela primaria pública, de organización completa, en la Ciudad de México. En cada clase, de una a dos horas de duración, yo me sentaba con un equipo de estudiantes para tomar notas y fotografías de sus producciones. Mientras tanto, una colega -a quien me refiero en el texto como “la observadora”- recorría con una cámara de video los distintos equipos de estudiantes y también hacía un registro de las anotaciones en el pizarrón y de las intervenciones de la maestra. Analicé las clases con herramientas de la teoría de las situaciones didácticas (Brousseau, 2007) y recurrí a trabajos que se acercan al aula desde perspectivas socioculturales. En muchas ocasiones, elegí fragmentos en los que intervienen estudiantes “con dificultades” –no he encontrado una manera adecuada de nombrarles-, pues en su actividad es donde se perciben con mayor claridad las contradicciones de un sistema educativo que al mismo tiempo incluye y excluye, como han explicado en otros trabajos McDermott (2001) y Terigi (2009).

En los siguientes apartados, me centraré en mostrar cómo la presión por llegar a las fórmulas, por un lado, hace que los procedimientos y las dudas de las y los alumnos tengan poco espacio en la clase y, por el otro, demanda la puesta en juego de conocimientos que muchas veces todavía están fuera de su alcance.

La tarea apunta a una fórmula, los alumnos piensan en figuras

Las tareas que plantea la maestra con la intención de abordar las fórmulas de área desatan una diversidad de procedimientos sobre los cuales las y los alumnos tienen mucho que explorar. Surgen múltiples dudas e ideas que no tienen que ver todavía con las fórmulas, sino con las transformaciones de unas figuras en otras, con las unidades de medida y con las figuras geométricas. A continuación, mostraré un ejemplo del último caso.

En una clase, las y los alumnos resuelven una lección del libro de texto oficial⁶ en la que se pide recortar un paralelogramo por la altura para transformarlo en un rectángulo y luego inferir la fórmula de área. Para ello, la primera consigna es trazar un paralelogramo igual a un modelo (Imagen 3) en una cuadrícula recortable, de manera que las niñas y los niños no recorten la página de la lección, sino la de la hoja cuadriculada ubicada al final del libro.

En un equipo están Analí y Leticia –dos alumnas con dificultades-, Ana y Héctor. A Analí, esa primera tarea de copiar el paralelogramo, que desde la lección se trata como un asunto accesorio y de fácil resolución, le toma toda la clase. Ella traza primero un trapecio (Imagen 4) y le sorprende que su figura se vea tan distinta a la original: “no me sale, tendría que haber hecho más para acá ¿no?”. La borra y entrega la cuadrícula en blanco a Leticia, para que ella le haga el trazo.

Imagen 3

Imagen 4

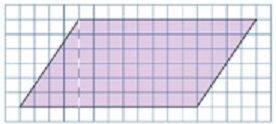
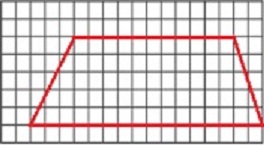
Leticia le regresa un paralelogramo distinto al del modelo, pues cambia el tamaño de la base y la inclinación. Analí acepta la figura, pero cuando la maestra le hace notar la diferencia de las bases, superpone la copia y el modelo y le explica cómo comenzar, ella concluye que “salió mal”. Es decir, en el primer caso del trapecio, Analí distingue por apreciación visual que algo no está bien; pero ahora que la vista no es suficiente, ella no recurre a empalmar su figura y el modelo, sino que la validación ocurre cuando interviene la maestra.

Ana y Leticia, que escuchan a la maestra, descartan el paralelogramo que habían hecho y vuelven a comenzar. Analí se levanta a pedir ayuda a Álvaro, un niño del equipo de al lado, pero él se niega. Héctor, quien se ha levantado de su asiento, regresa, superpone su paralelogramo al de la lección, no coinciden, lo refleja –es decir, lo voltea- y así tampoco embonan. Analí vuelve a hacer una figura y me la enseña: nuevamente, el primer impulso para validar no es el contraste entre las dos figuras, sino el reconocimiento de una persona adulta. La idea de que se puede comprobar la igualdad de dos figuras superponiéndolas no es tan natural como parecería, es algo que se aprende. Además, es probable que la validación empírica suponga para Analí una cierta confianza en lo que ella misma podrá percibir al hacerla. Yo le pido que haga la superposición; ella se levanta y va con la maestra, quien identifica errores comunes en varios de sus estudiantes y se dirige a todo el grupo para darles indicaciones.

Analí vuelve a su lugar y comienza a hacer un paralelogramo para Héctor, lo cual ejemplifica una manera suya de reaccionar frente a la dificultad. Cuando no puede con alguna tarea, suele pedir ayuda a sus pares; una ayuda que muchas veces le es negada. En cambio, ella tiende a ayudar, sobre todo a Pablo, su compañero con síndrome de Down, a quien le asignan tareas diferenciadas de menor complejidad. Es posible que se sienta menos vulnerable al asumir tareas que no le han sido asignadas a ella, o bien que seleccione tareas de las que puede hacerse cargo. Yo le explico que su figura es casi la que se ha pedido, pero que deslizó un cuadrito de más en el lado horizontal superior.

En ese momento, la maestra da una cuidadosa explicación al grupo sobre cómo hacer el trazo y lo ejemplifica con un dibujo en el pizarrón: hay que marcar primero la base y cuidar su longitud, luego considerar la altura y los cuadritos que hace falta “recorrer” –es decir, la inclinación-, para poder trazar el lado horizontal paralelo a la base, cuidando que ambos midan lo mismo, y después marcar los otros dos lados al unir los vértices. Analí no parece escuchar esa intervención de la maestra, que justamente da respuesta a las dificultades que ha enfrentado. Sentada de espaldas al pizarrón, trata una vez más de resolver por sí sola. Esta tendencia de Analí de no atender las indicaciones hechas al grupo entero o a su equipo, que también pude observar en las otras clases, llama la atención. ¿La razón por la que no incorpora las ayudas de la maestra es porque está concentrada resolviendo ella misma?, ¿o ha aprendido que las explicaciones dirigidas a todo el grupo no le sirven a ella? ¿Es su actitud un resultado de la práctica de asignar actividades diferenciadas a las niñas y los niños con dificultades? Es decir, ¿algunos aprenden que lo que se dice al grupo no va dirigido a ellos? Analí solo atiende las explicaciones que se dirigen a ella en particular; valida sus resultados a partir de alguien más, a quien reconoce por haber terminado sin errores o por ser una persona adulta; con frecuencia pide ayuda, que muchas veces no recibe; le cuesta trabajo hacerse cargo de sus tareas, pero se hace responsable de algunas asignadas a sus pares. Todo esto muestra, como explica McDermott (2001), que el nicho de quien “tiene dificultades” es socialmente construido, no inherente a la persona.

Analí casi obtiene un paralelogramo, pero uno de los lados inclinados se desliza dos cuadros y el otro tres, en lugar de cuatro como en el modelo (Imagen 5). Héctor, en cambio, ha hecho un nuevo paralelogramo que ahora sí coincide con el de la lección. Leticia y Ana también lo logran y lo recortan para transformarlo en un rectángulo.

Imagen 5

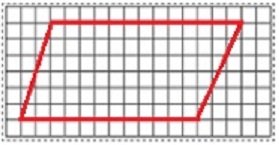
Finalmente, ayudo a Analí a resolver al poner su hoja cuadriculada sobre la figura de la lección y calcar los cuatro vértices. Analí se sorprende y se lamenta: “¿Por qué no pensé esto antes?”. Un poco después, cuando la clase está por terminar, Analí copia en su cuaderno las anotaciones que la maestra hizo en el pizarrón, que incluyen el dibujo de un paralelogramo y, una vez más, como al inicio, dibuja un trapecio: “Ay no me salió (…) miss, ¿me ayuda a hacer la figura esa?”.

En las seis figuras distintas por las que transita Analí se percibe su dificultad para reproducir el paralelogramo. Las figuras que ella traza tienen dos lados horizontales y otros dos inclinados, pero no parece tener presente que son paralelos. A sus pares también les cuesta trabajo copiar la figura. La detallada explicación de la maestra sugiere que ha identificado esa tarea como problemática para buena parte del grupo. La caracterización típica del paralelogramo como una figura que tiene dos pares de lados paralelos –obvia para quien la conoce bien-, así como las medidas que lo determinan, no son nada fáciles de percibir. Como muestra Fregona (1995), las propiedades del paralelogramo no son visibles de inmediato para las y los estudiantes; las figuras se enriquecen a partir de su experiencia con ellas. La tarea de copiar figuras, que en la lección se trata como sencilla y corta, podría dar pie a toda una situación didáctica con muchos aspectos por explorar para todo el grupo.

No se trata entonces de una dificultad específica de Analí, sino de algo que la mayoría necesita aprender. No obstante, hay diferencias entre Analí y sus compañeros de equipo. Una es que a ella la tarea de reproducir el paralelogramo le toma todo el tiempo de la clase. Para cuando termina, sus pares ya resolvieron la siguiente tarea, considerada desde la lección como central. Analí no aborda ese problema; copia las respuestas del libro de Ana, se peina, se estira un poco, sale al baño. Sensevy (2011) explica que la organización temporal escolar de los temas que hay que enseñar hace que muchas veces los conocimientos se aborden una única vez. Si un alumno o alumna se pierde un proceso de búsqueda en el momento designado para ello desde la enseñanza, hacer esa búsqueda después se considera inapropiado. Eso que en cierto momento se espera que todo el grupo haga, se vuelve algo vergonzoso cuando se hace a destiempo. Determinar un tiempo de aprendizaje implica que el tiempo que lo excede será destiempo y, en ese sentido, el destiempo se crea desde la institución. Ahora, Analí se ha perdido la posibilidad de buscar cómo calcular el área de un paralelogramo; después tendrá una sola oportunidad para hacerlo, seis clases más adelante.

Otra diferencia es que mientras sus pares logran resolver el trazo del paralelogramo como pueden –incluso calcando- y transformarlo en un rectángulo, al final de la clase ella aún se pregunta por qué le sale un trapecio. Analí tiene más dudas que el resto del grupo, y a partir de esta clase serán aún mayores, pues no se enteró de cómo se estableció la fórmula del área.

Por último, me interesa destacar que plantearse la pregunta de cómo llegar a una fórmula para calcular el área del paralelogramo implica reunir a todos los paralelogramos en un solo procedimiento. Esa infinidad de figuras –que pueden ser largas, achatadas, casi rectángulos, muy altas y delgadas o muy anchas y bajitas- se agrupan en una sola categoría de figuras que tienen dos pares de lados paralelos. Pero si Analí no logra ver de esta manera los paralelogramos, si no clasifica a las figuras de la manera que suponen las fórmulas, ¿qué sentido tiene para ella preguntarse por el área de ese tipo de figuras, y más aún, por una fórmula que las abarque? ¿Cuál es el propósito de disponer de un procedimiento genérico para una tarea que no ha resuelto y que se refiere a un tipo de figuras que todavía no agrupa en una categoría? Su participación en las siguientes clases implicará, por un lado, abandonar las preguntas sobre la reproducción de figuras y, por otro, aprenderse la fórmula, aplicarla y dar cuenta de ella en el examen.

La inquietud de Analí respecto a cómo copiar un paralelogramo es uno de muchos ejemplos. Frente a las tareas que se plantean desde la enseñanza con el propósito de arribar a las fórmulas para calcular áreas, las y los alumnos se ocupan de reproducir figuras; hacer configuraciones geométricas; comparar superficies de forma cualitativa –sin usar todavía números-; medir superficies mediante el conteo de unidades –al contar vértices en lugar de cuadros, hacer encuadramientos, cambiar la forma de la unidad para tener un número entero, reunir trozos de unidades para formar cuadros completos, hacer estimaciones-; transformar una figura en un rectángulo cuya área pueden calcular por conteo o mediante una multiplicación; hacer particiones de polígonos para dividirlos en triángulos y rectángulos cuya área saben determinar. Suelen pensar en el área de esa figura particular que tienen enfrente, no en un procedimiento genérico que les permita determinar el área de todo un tipo de figuras.

Así, a lo largo de las dieciocho clases, las y los alumnos del grupo despliegan numerosos procedimientos y surgen diversas preguntas y dudas relacionadas con el amplio universo de la medición con unidades y del estudio de las figuras en sí mismas, sin necesariamente medirlas todavía. La maestra hace un trabajo excepcional al dar cabida a toda esta diversidad de producciones; es una práctica que no siempre se observa en las aulas. Sin embargo, esa oportunidad no es suficiente para que las niñas y los niños profundicen, encuentren respuestas a sus preguntas, socialicen lo que hacen, enriquezcan su repertorio de procedimientos, e incluyan en dichos procedimientos algunos más cercanos a las fórmulas. Muy pronto se deja todo eso de lado porque la enseñanza del contenido curricular apremia.

La maestra percibe que sus estudiantes necesitan más tiempo para explorar los procedimientos y las nociones y, a veces, opta por dedicar otra clase al tema. Sin embargo, en otras ocasiones decide no hacerlo, a pesar de considerarlo necesario. La organización de la escuela graduada dificulta mucho la posibilidad de volver a estudiar conocimientos considerados anteriores a través de actividades nuevas, que los nuevos contenidos traen a escena.

La inteligibilidad de las fórmulas, un salto drástico para las y los alumnos

En el apartado anterior argumenté que, frente a las tareas previstas para acercarse a las fórmulas, las y los alumnos más bien movilizan conocimientos vinculados con las figuras y una diversidad de procedimientos para calcular su área, distintos de las fórmulas. Podría pensarse que, al fin y al cabo, en teoría, tendrían que haber aprendido esos contenidos en grados anteriores, y que, tal vez, aun sin disponer de ellos, las y los alumnos pueden utilizar las fórmulas de área, que es el contenido que corresponde a este grado según la prescripción curricular. Por ello, en este apartado y el siguiente me interesa mostrar lo que sucede cuando la maestra intenta evitar que se “desvíen” hacia otros conocimientos y adentrarlos en las fórmulas, o cuando las y los alumnos lo hacen por cuenta propia.

Como expliqué en la introducción, las fórmulas suelen introducirse en clase a partir de la relación “el área de un triángulo es la mitad del área de un rectángulo”. Esto con frecuencia se ejemplifica con un solo rectángulo dividido en dos triángulos rectángulos, y luego, sin más trámite, se generaliza a todos los triángulos (imágenes 1 y 2). Dicha generalización incluye los casos en que una de las tres alturas queda fuera del triángulo –es decir, los triángulos obtusángulos-, cuyo grado de complejidad ha sido mostrado por Douady y Perrin-Glorian (1989), pues la relación con el rectángulo es muy difícil de anticipar.

Un episodio entre Ana y Leticia –una alumna con dificultades- deja ver que incluso esa idea germinal no siempre es fácil de percibir. Leticia y Ana trabajan juntas muchas veces, y parece estar implícito que Ana sabe más; es ella quien marca la pauta de los procedimientos y hace un esfuerzo por explicarle con claridad a Leticia. En una clase intentan encontrar el área de seis triángulos rectángulos al reunir trozos para formar cuadros completos, por iniciativa de Ana (por ejemplo, Imagen 6).

En uno de los casos, Leticia le enseña a Ana su figura, que tiene otras marcas, y le dice: “Mira” (Imagen 7). Esa manera de desagregar el triángulo sugiere su transformación en un cuadrado (Imagen 8), pero Ana no parece interpretar ese “mira” como una aportación de su compañera; traza los dos segmentos auxiliares que Leticia no marcó. En la imagen que le muestra Leticia no ve un procedimiento distinto, más efectivo, sino rayitas que faltan.

Imagen 6

Imagen 7

Imagen 8

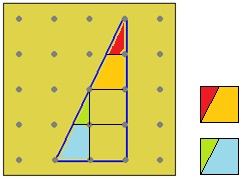
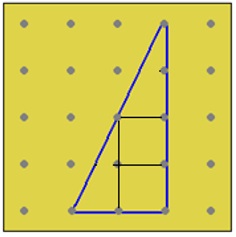
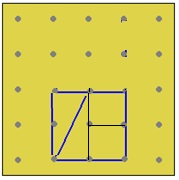
Tal vez, Ana está tan centrada en la desagregación en trozos, que aquello que le muestra Leticia no es suficiente para que logre ver otra cosa; así, más bien ve su propio procedimiento, pero inacabado. Con otros estudiantes pude observar que el paso del conteo de unidades al establecimiento de la relación entre una figura y un rectángulo implica un salto significativo; Ana aún está lejos de dar ese salto. A esto se agrega que, como en esa relación entre pares Ana es la “experta”, quizás no contempla la posibilidad de que alguien cuya imagen está más devaluada que la suya pueda hacer un aporte. Ana no se cuestiona lo que Leticia le quiere enseñar, sino lo que hay que corregirle. Leticia termina por seguir el conteo del cual Ana no desiste, ni siquiera cuando el procedimiento se complica de forma considerable. Poco después, llega la maestra y les sugiere hacer un rectángulo (imágenes 9 y 10).

Imagen 9

Imagen 10

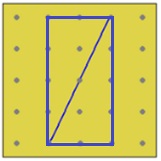
Luego trata de hacerles ver la ventaja de contar en el rectángulo, en lugar de en el triángulo:

1. 1. Maestra: ¿Qué es más fácil, contar cuadros completos o cortados por la mitad?⁷

2. 2. Ana: Ehhhhh…. contar los cuadros por la mitad.

3. 3. Leticia: [en voz muy baja, al mismo tiempo que Ana] Contarlos completos

   (…)

4. 4. Maestra: Eso está bien, ahí ya van bien. ¿Entonces qué hacemos para contar los cuadros completos? ¿Contamos el triángulo o, o, o contamos lo del rectángulo?

5. 5. Ana: Lo del triángulo.

6. 6. Maestra: ¿En el triángulo sí tiene los cuadros completos?

7. 7. Ana: Ah, no.

8. 8. Leticia niega con la cabeza.

9. 9. Maestra: Entonces, ¿qué es más fácil?

10. 10. Ana y Leticia: En el rectángulo.

    (…)

11. 11. Leticia: ¡Porque el triángulo es la mitad del rectángulo!

12. 12. Ana: [al mismo tiempo que Leticia, en voz muy baja] [inaudible] Del rectángulo

    (…)

13. 13. Maestra: ¿Cómo podemos conocer cuánto tiene de superficie entonces éste?

14. 14. Ana: Mmmhhh… ¿dividir? (…) dooos entreeeee... (…) ¿dos entre ocho?

    (…)

15. 15. Leticia: (…) en el rectángulo tengo ocho… (y en el triángulo) mmmmh…. ¡cuatro!

La maestra intenta hacerles ver que el triángulo es la mitad del rectángulo, relación que facilita el cálculo del área del primero. Esta decisión es comprensible, no solo porque para ella es muy evidente, sino también porque ha visto a las dos alumnas instaladas en el conteo de unidades. Calcular áreas de esa manera se vuelve largo y difícil, pues las formas globales de los trozos difieren mucho de una figura a otra, así que al unirlos en un triángulo rectángulo no queda claro cuáles hay que asociar en el siguiente. Duplicar la figura engloba a todos los triángulos rectángulos en un mismo procedimiento en el que solo hay que contar cuadros completos. No sé si la maestra piensa en esa ventaja, o bien en que, a diferencia del conteo de cuadros, esa manera de resolver puede traducirse a una fórmula.

Sin embargo, Ana experimenta ese cambio de procedimiento de una manera distinta. De entrada, ella no trae a escena al rectángulo; es la maestra quien sugiere trazarlo. Una vez trazado, su utilidad no queda clara; si bien parece que la alumna balbucea la relación “el triángulo es la mitad del rectángulo” (línea 12), no la vincula con el problema que debe resolver. Ana sigue centrada en el triángulo; elige contar por “mitades” y hacerlo en el triángulo (líneas 2 y 5), como en un principio. Para ella no es evidente que ahí hay un rectángulo y que el área de ese rectángulo es el doble del área del triángulo. Tampoco lo es que contar en el rectángulo es mucho más sencillo que en el triángulo. Existe una tensión entre lo que ve la maestra y lo que ve la alumna; lo que para una es obvio y está ahí, para la otra no existe todavía, en el sentido de que no es parte del medio, de las herramientas con las que cuenta para resolver. La posibilidad de remitir el área del triángulo a la del rectángulo implica un trabajo espacio-geométrico que no es menor; es necesario dejar de ver lo que está –el triángulo-, para ver lo que no está –el rectángulo-.⁸ Pasar del conteo cuadro por cuadro a la relación entre una figura y un rectángulo implica ver las figuras de otra manera, mirar nuevas figuras y nuevas relaciones entre las mismas.

Leticia se muestra más receptiva al cambio de procedimiento que sugiere la maestra cuando responde que es mejor contar los cuadros completos en el rectángulo (líneas 3 y 10). Antes, al resolver solas la tarea, Leticia estaba menos aferrada al conteo trozo por trozo que su compañera; quizás por eso le es más fácil modificar la manera de resolver. Como muestra Sadovsky (2003), las y los alumnos que participan menos en la construcción de un procedimiento se muestran más dispuestos a despegarse de él para evaluar los de otros. Además, me parece importante recordar que, al parecer, Leticia ya anticipaba una relación triángulo-cuadrado parecida a la que les propone ahora la maestra, cuya presencia parece ayudar a validar esa relación. Al inicio, Leticia responde las preguntas después de Ana o en voz más baja, pero no contesta lo mismo: disiente de su compañera y se afilia más a lo que propone la maestra. Más adelante dice, con seguridad: “¡El triángulo es la mitad del rectángulo!” (línea 11). La intervención de la maestra parece ayudarle a posicionarse frente a su compañera de otra manera. El fragmento anterior muestra que la relación novata-experta entre las alumnas no es rígida, se modifica cuando cambia el contexto de interacción.

Douady y Perrin-Glorian (1989) analizan las relaciones entre el conteo de unidades y el procedimiento de recubrimiento, que consiste en transformar una figura en otra equivalente en superficie al cortar pedazos y reacomodarlos sin empalmarlos ni dejar huecos. La transformación de una figura en un rectángulo es un caso particular de esta manera de comparar superficies. Al diseñar una primera secuencia didáctica, las autoras apostaron por el recubrimiento, que les parecía más fecundo porque contribuye a disociar la superficie de la forma global de una figura, mientras que, en el conteo de unidades, al mantenerse fija la forma, esto no sucede. No obstante, al observar la actividad de las niñas y los niños en la secuencia y en las entrevistas, cambiaron de opinión; es necesaria la interacción entre el “papel blanco” de las transformaciones y el “papel cuadriculado” del conteo de unidades. Esto porque, cuando las y los alumnos aún tienen que aprender que el recubrimiento conserva la superficie, tienen incertidumbre sobre ese procedimiento y, en esos casos, el conteo de cuadros permite validar las resoluciones.

A la luz de este trabajo, la idea de una interacción entre el papel cuadriculado y el blanco me hace mucho sentido. Por un lado, las cuadrículas son importantes porque muchos estudiantes están todavía en el conteo de cuadritos y aún tienen varias preguntas por responder. En cambio, las transformaciones se encuentran muy lejos de lo que hace la mayoría. Por otro lado, tener más experiencia con las transformaciones y, más en general, con el recubrimiento, ayudaría a que las y los alumnos construyan una idea sobre «tener la misma superficie», que pase por la cantidad de espacio, no por los números. Eso sería importante tanto para separar la superficie de la forma global de las figuras como para acceder a las fórmulas. Aunque esa interacción entre las cuadrículas y el recubrimiento podría ser muy fructífera, su construcción no es sencilla; requeriría, de entrada, un tiempo que, en términos institucionales, es difícil de gestionar.

El episodio de Ana y Leticia muestra las dificultades para comprender la relación “el área de un triángulo es la mitad del área de un rectángulo”, a partir de la cual se generan las fórmulas en las clases. En otros casos, vi estudiantes que, aunque sí ponían en juego dicha relación, no la vinculaban a la fórmula. El procedimiento geométrico y la regla algebraica aparecen como dos conocimientos que no se tocan. El primero es funcional y se usa para determinar áreas; la segunda tiene legitimidad, pasa al cuaderno con un lenguaje especializado y se debe aprender para el examen.

Acceso desigual de las y los alumnos al uso de fórmulas

Cuando las tareas exigen como único procedimiento el uso de una fórmula, o incluso cuando las y los alumnos la eligen, surgen múltiples errores. Uno de los más importantes tiene que ver con la identificación de líneas auxiliares que, de inicio, no están en las figuras, pero sí en las fórmulas: diagonales, alturas, radios y apotemas.

En una clase, a sugerencia de la maestra, Marina –una alumna con dificultades- se sienta con Mora y Valentina. Deben encontrar el área de distintas figuras, tarea para la que hay varios procedimientos posibles, pues las figuras están trazadas en una cuadrícula. Desde la primera figura, Valentina da por sentado el uso de la fórmula, y las otras dos la siguen. La fórmula es un procedimiento que muy pronto se hace presente; es una expectativa institucional constante, que tiene más peso para algunos estudiantes que para otros.

Dado que se trata de un triángulo, el uso de la fórmula involucra la altura, la cual no es nada fácil de ver. Aunque Valentina sabe cuál es la fórmula que tienen que usar, toma uno de los lados como la altura, una asociación muy común, que trabajos como el de Castaño (2021) han puesto de manifiesto. Así, multiplica las longitudes de dos lados, y sus compañeras hacen lo mismo. Al hacer la cuenta a mano, el primer resultado parcial las hace dudar, pero no saben cómo continuar. Esto detiene a Marina, quien deja de anotar en su hoja; en cambio, Mora y Valentina recurren a la calculadora.

Cuando van a revisión con la maestra, ella deja claro que la respuesta “está mal”, pues la altura va de “la base a la punta más alta (…) pero no se mide chueco”. Esto desata una larga interacción cíclica: las alumnas, sobre todo Valentina, señalan otro de los lados; la maestra vuelve a indicar que hay un error; entonces ellas señalan el otro lado. En ese intercambio, la maestra hace una formulación que refleja una característica de la altura. Les dice, “Para usar la fórmula tuviste que calcular… calcular la altura, ¿la tomaste?”. Es interesante la pausa que hace, su titubeo con la palabra “calcular”. La altura no es una medida que se obtiene al hacer cálculos con las medidas que se tienen, como en el caso del área. Pero tampoco se mide directamente con la regla, como se hace con los lados, porque no está trazada de antemano. Más adelante, la maestra utiliza una palabra más adecuada: “encontrar” la altura (“Entonces tendrías que haber encontrado primero tu altura, si no, ¿cómo lo hiciste?”).

Al inicio, Valentina se muestra segura (“Ajá, sí, aquí está [la altura]”), pero a medida que sus respuestas son rechazadas por la maestra, se torna más titubeante (“aaaaah, ésta es”). Aunque siempre identifica a la altura con uno de los lados, percibe que no es la respuesta esperada. El error puede ser resultado, en parte, de la tendencia a enseñar la fórmula del triángulo a partir del triángulo rectángulo. En ese caso, la altura sí coincide con uno de los lados. ¿Cómo podrían inferir las y los alumnos que en la mayoría de los triángulos eso no sucede? Y si esa práctica de enseñanza está tan extendida, ¿cómo podría la maestra percibir que genera confusión entre sus estudiantes? Para la maestra, la coincidencia entre la altura y un lado es un caso particular, un ejemplo excepcional en el amplio universo de los triángulos; sin embargo, para las alumnas es el caso general. Para la maestra, la altura es un segmento distinto a los lados, que “no se mide chueco”, idea en la que puede estar implícita la perpendicularidad de la altura respecto a la base. Sin embargo, para las alumnas, es un lado. Al hablar de altura, la maestra y las alumnas se refieren a objetos distintos. Finalmente, en cierto momento, la maestra interpela de forma directa a Valentina, quien, por alguna razón, señala el segmento esperado.

La altura es problemática para todo el grupo. Una vez más, no se trata de un asunto relativo a estudiantes con dificultades, sino de una noción compleja. Sin embargo, hay diferencias entre la actividad de las tres alumnas. La interacción con la maestra ofrece a Valentina un bote salvavidas; Marina y Mora no tienen la misma suerte. Valentina intenta poner en marcha un procedimiento que ha elegido; sus compañeras tratan de adherirse a esa decisión. Cuando las cuentas a mano fallan, Valentina y Mora tienen una calculadora; Marina no. Por último, Valentina es la principal interlocutora de la maestra. En ninguna otra clase observé que Marina pudiera identificar la altura de una figura.

¿Es posible que una interacción distinta entre las alumnas y la maestra hubiera derivado en que Marina también encontrara la altura? Mi apuesta es que no; o, en todo caso, no habría sido suficiente para detectarla en otras figuras. La dificultad para construir la noción de altura radica, precisamente, en eso que al parecer intuye la maestra cuando no le convencen las palabras “calcular” ni “tomar”, o cuando insiste en que la altura no es un lado. Reparar en la altura requiere dejar de ver los segmentos que están trazados, que se han medido y con cuyas medidas se ha operado para ver algo que hasta ese momento no existía.

Ese cambio en la mirada es tan importante que, de hecho, modifica la noción de triángulo. Perrin-Glorian y Godin (2018) plantean a estudiantes un problema que implica hacer un esquema de la entrada al museo del Louvre –una pirámide cuadrangular-, a partir de una fotografía. La colocación de la altura en dicho esquema lleva a “transformarlo en una representación de un objeto geométrico” (p. 11). Es decir, es al poner la altura que un objeto material del espacio sensible deviene en uno conceptual; el esquema ya no representa una parte del museo, sino una pirámide.

Además, la fórmula incluye las tres posibles alturas de un triángulo, pero en este fragmento se habla de una sola base y una sola altura. Perrin-Glorian (1999) afirma que, de hecho, las y los alumnos solo se convencen de la fórmula cuando encuentran que el resultado es el mismo para las tres alturas. A Mora, Valentina y Marina les cuesta trabajo encontrar una altura, y parecen asumir que es la única. El asunto de las tres alturas no es objeto de estudio.

En las clases que observé, fueron pocas las veces en que las y los alumnos usaron la altura como un elemento necesario para resolver un problema. Sin embargo, de pronto, las tareas que demandan deducir o aplicar una fórmula suponen su presencia explícita, nombrada, clara y fundamental. En este sentido, la altura pasa de no existir, a tener una existencia absoluta. Hace falta un momento intermedio en el que aparezca como algo funcional pero implícito, como el segmento por el que conviene cortar una figura para transformarla en un rectángulo (Douady y Perrin-Glorian, 1989). La altura emerge como un objeto funcional cuando las y los alumnos deben ocuparse de la superficie en el marco geométrico. Si ese marco se deja de lado, se pierde de vista precisamente aquello que la fórmula mide: la superficie. Se cuenta entonces con la técnica, pero no es claro para qué sirve. Es decir, ese número que resulta –el área- no es portador del tamaño de la superficie de la figura.

Reflexiones finales: la pertinencia de posponer el estudio de las fórmulas

A lo largo de este trabajo, he mostrado algunas condiciones institucionales que dificultan para la mayoría de las y los alumnos –no solo para quienes tienen dificultades- el acceso a las fórmulas y su uso. A la vez, esas mismas condiciones demandan el dominio de dichas fórmulas.

Esta contradicción lleva a una práctica en la que la jerga matemática es cada vez más amplia y, muchas veces, carece de sentido. En las clases que presencié, después de anotar todos los términos que resultaban problemáticos para las y los alumnos, obtuve esta lista:

área, fórmula, perímetro, volumen, áreas laterales, superficie, romboide, rectángulo, cuadrado, trapecio, rombo, pentágono, triángulo, triángulo isósceles, triángulo escaleno, triángulo equilátero, cubo, círculo, polígono inscrito, pentágono regular, hexágono regular, octágono regular, prisma, cuadrilátero, polígono, paralelogramo, prisma triangular, prisma rectangular, polígono regular, pirámide, cuerpo geométrico, figura plana, tridimensional, dimensiones, ancho, largo, profundidad, altura, base, apotema, diagonal, vértice, base mayor, base menor, cara, arista, cara lateral, base triangular, base pentagonal, diagonal mayor, diagonal menor, radio, diámetro, circunferencia, ángulo, ángulo obtuso, ángulo oblicuo, sagito, cuerda, unidades cuadradas, metros cuadrados, grados, transportador, paralelismo, líneas paralelas, pi.

Desde la organización curricular, se esperaría que las niñas y los niños de quinto grado estuvieran familiarizados con la mayoría de estas nociones. Sin embargo, esto no sucede. La lista sería seguramente mucho más larga si le sumáramos las nociones problemáticas vinculadas a otros temas de matemáticas y a otras asignaturas. Mi percepción es que, al no disponer del tiempo que las y los alumnos necesitan para dotar de sentido al establecimiento y uso de contenidos como las fórmulas, se van acumulando los conocimientos que aún no han aprendido, pero se esperaría que ya dominaran. Esto genera un conflicto permanente para la maestra.

La maestra tiene que enseñar cierto contenido en un tiempo establecido, bajo condiciones que la mantienen en una tensión constante, entre las que destacan las lecciones que no favorecen ese aprendizaje. Ninguna de las propuestas a las que la maestra accede, oficiales o particulares, permite a sus estudiantes explorar realmente todo lo que necesitan para poder decir, con sentido, “el área del triángulo es la mitad del área de un rectángulo”.⁹ Esas tensiones terminan por afectar a las y los alumnos; los fracasos en las tareas no se ven como el efecto de una serie de condiciones institucionales contradictorias, sino como deficiencias personales. En este proceso, se invisibilizan los conocimientos que están implicados en la actividad de las y los alumnos, pero tienen poca presencia curricular; y, en cambio, se priorizan las fórmulas, que son todavía inaccesibles para la mayoría.

Referencias bibliográficas

Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas. Buenos Aires: Libros del Zorzal.

Burke, C. y Grosvenor, I. (2013). The Steward Street School experiment: a critical case study of possibilities. British Educational Research Journal, 39(1), 148–165.

Castaño, Y. (2021). Trabajo colaborativo entre profesores de secundaria e investigadores. Una experiencia en torno a la caracterización y congruencia de figuras geométricas (Tesis de Maestría). Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, Ciudad de México, México.

Chartier, A.-M. (2004). Enseñar a leer y escribir. Una aproximación histórica. México: Fondo de Cultura Económica.

Douady, R. y Perrin-Glorian, M. J. (1989). Un processus d’apprentissage du concept d’aire de surface plane. EducationalStudies in Mathematics, 20(4), 387–424.

Fregona, D. (1995). Les figures planes comme “milieu” dans l’enseignement de la géométrie: interactions, contrats et transpositions didactiques (Tesis de Doctorado). Université Bordeaux I, Burdeos, Francia.

Grimaldi, V. (2021). La construcción de la colaboración en un aula de Matemática del nivel secundario. Análisis de una experiencia. En P. Cobeñas, V. Grimaldi, C. Broitman, I. Sancha y M. Escobar (Coords.) La enseñanza de las matemáticas a alumnos con discapacidad (pp. 413-449). La Plata: Edulp.

McDermott, R. (2001). The acquisition of a child by a learning disability. En J. Collins y D. Cook (Eds.), Understanding Learning: Influences and Outcomes (pp. 60–70). Thousand Oaks: SAGE Publications Inc.

Mendoza von der Borch, T. M. (2021). De las figuras geométricas a las fórmulas de área. Tensiones entre conocimientos de los alumnos y contenidos curriculares (Tesis Doctoral). Departamento de Investigaciones Educativas del Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, Ciudad de México, México.

Moreira Baltar, P. (1996-1997). A propos de l’apprentissage du concept d’aire. Petit X, 43, 43–68.

Perrin-Glorian, M. J. (1999). Le problème de l’enseignement des mesures des grandeurs géométriques à partir de l’exemple des aires. Disponible en https://hal.archives-ouvertes.fr/hal-01385025/document

Perrin-Glorian, M. J. y Godin, M. (2018) Géométrie plane: pour une approche cohérente du début de l’école à la fin du collège. Disponible en https://hal.archives-ouvertes.fr/hal-01660837v2/document

Rockwell, E. (2021). “El emporio celestial de conocimientos benévolos”: Dilemas entre el currículo y la inclusión. Cuadernos de Educación, 19(19), 13–26.

Sadovsky, P. (2003). Condiciones didácticas para un espacio de articulación entre prácticas aritméticas y prácticas algebraicas (Tesis Doctoral). Universidad de Buenos Aires, Buenos Aires, Argentina.

Sensevy, G. (2011). Le sens du savoir. Eléments pour une théorie de l’action conjointe en didactique. Bélgica: Groupe de Boeck.

Solares Rojas, A. (noviembre, 2017). Estudio comparativo 2015 de las propuestas curriculares de Matemáticas en la educación obligatoria en México y otros países. Lo aprendido y lo que queda pendiente. Ponencia presentada en el XIV Congreso Nacional de Investigación Educativa. San Luis Potosí, México.

Terigi, F. (2009). El fracaso escolar desde la perspectiva psicoeducativa: hacia una reconceptualización situacional. Revista iberoamericana de educación, 50, 23-39.

Weiss, E., Block, D., Civera, A., Dávalos, A. y Naranjo, G. (2019). La enseñanza en educación básica. Análisis de la práctica docente en contextos escolares. México: Comisión Nacional para la Mejora Continua de la Educación.

Notas

Obra bajo Licencia Creative Commons Atribución-NoComercial-CompartirIgual 4.0 Internacional